Problem
You are given two sorted arrays A and B of lengths m and n, the task is to merge the two sorted arrays in such a way that the merged array is also sorted.
Example
Input
A[] = {3, 9, 10, 18, 23}
B[] = {5, 12, 15, 20, 21, 25}
Output
Merged[] = {3, 5, 9, 10, 12, 15, 18, 20, 21, 23, 25}
Explanation
The merged array is of the size of n + m and contains both the elements of array A and array B in sorted order
Input:
A[] = { 5, 8, 9}
B[] = {4, 7, 8}
Output:
Merged[] = {4, 5, 7, 8, 8, 9}
Explanation
The merged array is of the size of n + m and contains both the elements of array A and array B in sorted order
Brute Force Approach
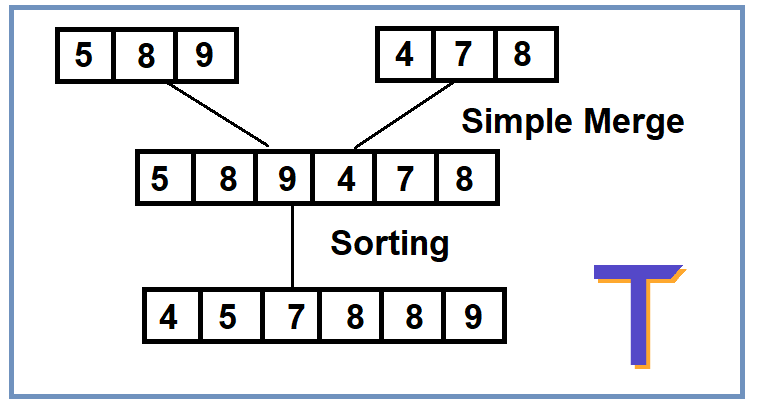
The idea is to create a new array C[] of length m+n and put all the elements from A[] and B[] in it and then sort them using Arrays.sort().
Algorithm
- Create an array C of n+m size to store the merged array
- Put the values of both A and B arrays using a for loop
- Sort the C array using Array..sort().
Pseudo Code
Int[] solve(int[] A, int[] B, int n, int m) {
Create a new array C of n+m size
while(i<n) {
C[k++] = A[i++];
}
while(j<m) {
C[k++] = B[j++];
}
Sort C;
return C
}
C++
#include<bits/stdc++.h>
using namespace std;
void mergeArrays(int arr1[], int arr2[], int m,
int n)
{
int i = 0, j = 0, k = 0;
int C[m+n];
// traverse the arr1 and insert its element in C
while(i < m){
C[k++] = arr1[i++];
}
// now traverse arr2 and insert in C
while(j < n){
C[k++] = arr2[j++];
}
// sort the whole array C
sort(C, C+m+n);
cout << "Array after merging" <<endl;
for (int i=0; i < m+n; i++)
cout << C[i] << " ";
}
// Driver code
int main()
{
int arr1[] = {1, 3, 5, 7};
int m = sizeof(arr1) / sizeof(arr1[0]);
int arr2[] = {2, 4, 6, 8};
int n = sizeof(arr2) / sizeof(arr2[0]);
mergeArrays(arr1, arr2, m, n);
return 0;
}
JAVA
package com.Tekolio.Sorting;
import java.util.*;
class Merge_two_sorted_arrays{
public static int[] mergeArrays(int[] A, int[] B, int m,int n){
int i=0, j=0, k=0;
int[] C = new int[m+n];
while(i<m) {
C[k++] = A[i++];
}
while(j<n) {
C[k++] = B[j++];
}
Arrays.sort(C);
return C;
}
public static void main (String[] args){
int[] A = {1, 3, 5, 7};
int m = A.length;
int[] B = {2, 4, 6, 8};
int n = B.length;
int[] nums = mergeArrays(A, B, m, n);
System.out.println("Array after merging");
for (int i=0; i < m+n; i++)
System.out.print(nums[i] + " ");
}
}
Python
def mergeArrays(nums1, nums2, m, n):
#create an empty array for storing result
nums3 = [None] * (m+n)
i = 0
j = 0
k = 0
#copy element of nums1[] to nums3[]
while i < m:
nums3[k] = nums1[i];
k = k + 1
i = i + 1
# Store remaining elements
# of second array
while j < n:
nums3[k] = nums2[j];
k = k + 1
j = j + 1
print("Array after merging")
for i in nums3:
print(nums3[i])
# Driver code
nums1 = [1, 3, 5, 7]
m = len(nums1)
nums2= [2, 4, 6, 8]
n = len(nums2)
#call function to merge sorted arrays
mergeArrays(nums1, nums2, m, n)
Output
Array after merging - 1 2 3 4 5 6 7 8
Time Complexity – O((m+n) log(m+n))
We have sorted an array of size m+n using Arrays.sort(), and the time complexity of this operation is O(n logn) which in this case becomes O((m+n )log(m+n))
Space Complexity – O(m+n)
We have created a new array C of size n+m which will store the merged sorted array.
Insertion Sort Approach
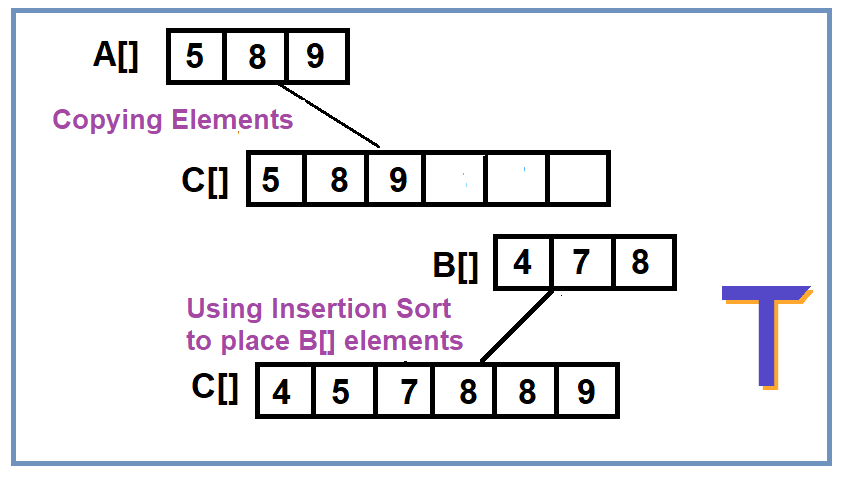
The idea here is the same as the brute force approach, we will first create a new array of n+m size and then put elements of A[] and B[] into it. But this time we will sort the while putting elements of B[] using insertion sort.
Algorithm
- Create an array C of n+m size to store the merged array
- Copy all the elements of A[] into C[]
- Now traverse the elements of B[] and insert elements one by one to C[] by using the insertion sort.
Pseudo Code
Int[] solve(int[] A, int[] B, int n, int m) {
Create a new array C of n+m size
while(i<n) {
C[k++] = A[i++];
}
for(i=0 -> m( {
Temp = B[i]
j=n-1
while(j>0) {
if(temp<C[j {]
C[j+1] = C[j]
}
else break
j–
}
n=m+1
C[j+1]=temp
}
return C
}
C++
#include <iostream>
using namespace std;
void merge_two_sorted_arrays(int A[], int B[], int m, int n) {
//Creating an array of size m+n to store a merged array
int C[m+n];
// copy A[] elements to C[]
for(int i=0;i<m;i++)
C[i]=A[i];
//apply insertion sort algorithm to insert B[] element in C[]
for(int i=0;i<n;i++){
int temp=B[i];
int j=m-1;
for(;j>=0;j--){
//move elments one position ahead that are greater than current value
if(C[j]>temp){
C[j+1]=C[j];
}
else
break;
}
m=m+1;
//put Current element at its correct position.
C[j+1]=temp;
}
// printing the resultant array
cout << "Array after merging" <<endl;
for(int i=0;i<m;i++)
cout<<C[i]<<" ";
}
int main(){
// The driver code
int A[] = {1, 3, 5, 7};
int B[] = {2, 4, 6, 8};
int m = sizeof(A) / sizeof(A[0]);
int n = sizeof(B) / sizeof(B[0]);
// calling our function
merge(A, B, m, n);
return 0;
}
JAVA
package com.Tekolio.Sorting;
class Merge_two_sorted_arrays{
// function to merge arrays
public static int[] mergeArrays(int[] A, int[] B, int m,int n, int[] C){
// copy A[] elements to C[]
for(int i=0;i<m;i++)
C[i]=A[i];
// apply insertion sort algorithm to insert B[] elements to A[]
for(int i=0;i<n;i++) {
int temp=B[i];
int j=m-1;
for(;j>=0;j--){
//move elments one position ahead that are greater than current value
if(C[j]>temp){
C[j+1]=C[j];
}
else
break;
}
m=m+1;
//put Current element at its correct position.
C[j+1]=temp;
}
return C;
}
// driver code
public static void main (String[] args){
int[] A = {1, 3, 5, 7};
int m = A.length;
int[] B = {2, 4, 6, 8};
int n = B.length;
int[] C = new int[m+n];
// calling function to merge two sorted arrays
mergeArrays(A, B, m, n, C);
// printing the resultant sorted array
System.out.println("Array after merging");
for (int i=0; i < m+n; i++)
System.out.print(C[i] + " ");
}
}
Python
def mergeArrays(A, B, m, n):
#create an empty array for storing result
C = [None] * (m+n)
i = 0
j = 0
k = 0
#copy element of A[] to C[]
while i < m:
C[i]=A[i]
i=i+1
i=0
#Apply insertion sort algorithm to insert B[] elements into C[]
while i<n:
t=B[i]
j=m-1
while j>=0:
#move elements one position ahead that is greater than the current value
if C[j]>t:
C[j+1]=C[j]
else:
break
j=j-1
m=m+1
#put Current element at its correct position.
C[j+1]=t
i=i+1
#print resultant array
print("Array after merging")
for i in C:
print(str(i), end = " ")
# Driver code
A = [1, 3, 5, 7]
m = len(A)
B= [2, 4, 6, 8]
n = len(B)
#call function to merge sorted arrays
mergeArrays(A, B, m, n)
Output
Array after merging - 1 2 3 4 5 6 7 8
Time Complexity: O(m*n)
In the above code, the first loop is used to copy all the elements of A[] into C[], and this process takes O(n) time. While the second loop copies all the elements of B[] into C[] which have been sorted while copying using insertion sort which takes O(n*m) time.
Space Complexity: O(n+m).
We have created a new array C of size n+m which will store the merged sorted array.
Efficient Approach – Merge Sort with O(n+m) time
This approach is somewhat similar to the above two approaches as here also we need to make an array of size m+n and put the two sorted arrays into it. But this time we will be doing both tasks simultaneously – sorting and copying elements with the help of merge sort. The idea is to traverse both arrays at the same time using two pointers i and j while keeping the third pointer k at the C[] where we have to put the elements.
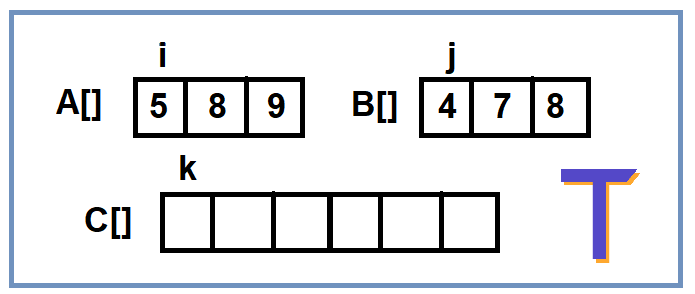
Now we have to check which element is smaller from both the arrays and put that element in C[] at the kth index. After this, we will increase the kth pointer as well as the pointer of the array which had the smallest element among them.
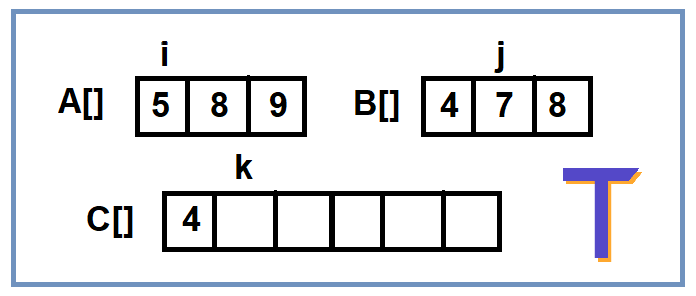
This process will continue until we have reached the end of one of the arrays.
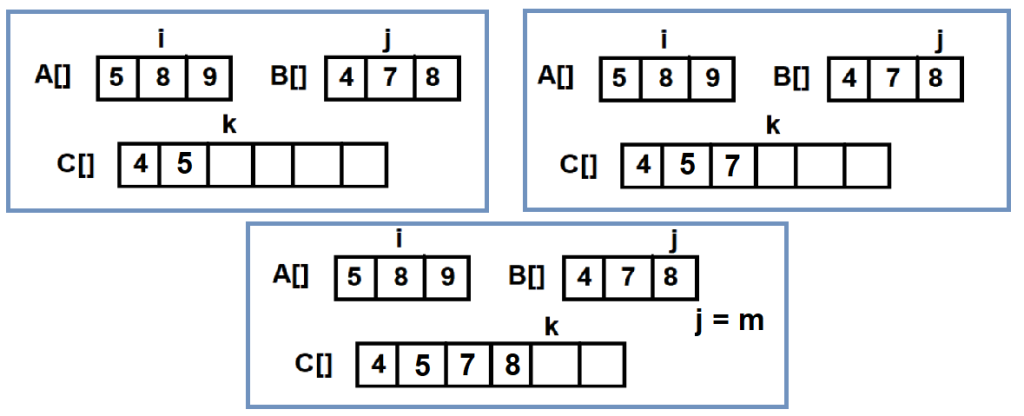
And as for the other array, we will just append the remaining elements at the end of the C[] as it is as the given arrays are already sorted.
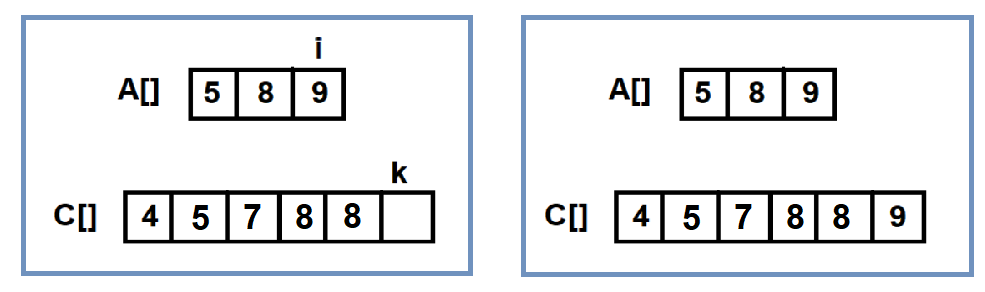
Algorithm
- Create an array C of n+m size to store the merged array
- Initialize three pointers i, j, and k for the three arrays respectively.
- Traverse both the input arrays simultaneously using the pointers.
- Compare the elements of both arrays at each index using the pointers and place the smaller one into the C[].
- Increase the pointer of that array through which we have copied the element for C[] and the pointer of the C[].
- If we have reached the end of any array, simply copy the remaining elements of the other array and paste them into C[].
Pseudo Code
Int[] solve(int[] A, int[] B, int n, int m) {
Create a new array C of n+m size
Int i, j, k
while(i<n && j<m) {
if(A[i]<B[j]) {
C[k++]=A[i++]
} else {
C[k++]=B[j++]
}
}
while (i < n1) {
C[k++] =A[i++];
}
while (j < n2) {
C[k++] =B[j++];
}
return C
}
C++
#include<iostream>
using namespace std;
// Merge A[0..m-1] and B[0..n-1] into
// nums3[0..m+n-1]
void mergeArrays(int A[], int B[], int m,int n){
int i = 0;
int j = 0;
int k = 0;
int C[m+n];
// Traverse both array
while (i<m && j <n){
// Check if current element of first
// array is smaller than current element
// of second array. If yes, store first
// array element and increment first array
// index. Otherwise do same with second array
if (A[i] < B[j])
C[k++] = A[i++];
else
C[k++] = B[j++];
}
// Store remaining elements of first array
while (i < m)
C[k++] = A[i++];
// Store remaining elements of second array
while (j < n)
C[k++] = B[j++];
cout << "Array after merging" <<endl;
for (int i=0; i < m+n; i++)
cout << C[i] << " ";
}
// Driver code
int main(){
int A[] = {1, 3, 5, 7};
int m = sizeof(A) / sizeof(A[0]);
int B[] = {2, 4, 6, 8};
int n = sizeof(B) / sizeof(B[0]);
mergeArrays(A, B, m, n);
return 0;
}
JAVA
class Main{
public static int[] mergeArrays(int[] A, int[] B, int m,int n){
int i = 0, j = 0, k = 0;
int[] C = new int[m+n];
// Traverse both array
while (i<m && j <n){
// Check if current element of first
// array is smaller than current element
// of second array. If yes, store first
// array element and increment first array
// index. Otherwise do same with second array
if (A[i] < B[j])
C[k++] = A[i++];
else
C[k++] = B[j++];
}
// Store remaining elements of first array
while (i < m)
C[k++] = A[i++];
// Store remaining elements of second array
while (j < n)
C[k++] = B[j++];
return C;
}
public static void main (String[] args){
int[] A = {1, 3, 5, 7};
int m = A.length;
int[] B = {2, 4, 6, 8};
int n = B.length;
int[] nums = mergeArrays(A, B, m, n);
System.out.println("Array after merging");
for (int i=0; i < m+n; i++)
System.out.print(nums[i] + " ");
}
}
Python
def mergeArrays(A, B, m, n):
C = [None] * (m+n)
i = 0
j = 0
k = 0
# Traverse both array
while i < m and j < n:
# Check if current element of first array is smaller than current element of second array. If yes, store first array element
# and increment first array index. Otherwise do same with second array
if A[i] < B[j]:
C[k] = A[i]
k = k + 1
i = i + 1
else:
C[k] = B[j]
k = k + 1
j = j + 1
# Store remaining elements of first array
while i < m:
C[k] = A[i];
k = k + 1
i = i + 1
# Store remaining elements of second array
while j < n:
C[k] = B[j];
k = k + 1
j = j + 1
print("Array after merging")
# for i in range(m+n):
print(str(C[i]), end = " ")
# Driver code
A = [1, 3, 5, 7]
m = len(A)
B = [2, 4, 6, 8]
n = len(B)
mergeArrays(A,B, m, n);
Output
Array after merging - 1 2 3 4 5 6 7 8
Time Complexity: O(n+m)
As we are simply traversing both arrays simultaneously, the time complexity becomes O(m+n). Then we have to store the remaining elements into the C[] which again take a time of O(n) or O(m) depending upon which array has remaining elements.
Space Complexity: O(n+m)
We have created a new array C of size n+m which will store the merged sorted array.

