Problem Statement
We are given three integers n, r, and p, we have to find the value of nCr%p. Here p is a natural number greater than n and nCr is the Binomial Coefficient.
Examples
Input: n = 10, r = 2, p = 13
Output: 6
Explanation: 10C2 is 45 and 45 % 13 is 6.
Well, there are many ways of solving this problem, but in this blog, we will only discuss 3 of them as according to us they are the easier ones to understand among all.
Also, see solving nCr%p in O(n) time complexity with Fermat’s Little Theorem – but this is only valid when p is a prime number
Brute Force Approach
The brute force approach is very simple just find the nCr of the given number and take the mod of that number with p and print the result.
We will be using one of the properties of Combinations to solve nCr.
nCr = n-1Cr-1 + n-1Cr
The below code is the implementation of the brute force approach using recursion
JAVA
package com.Tekolio.Extras;
// solve nCr%p
public class solve_cobnimatrics_1 {
public static void main(String[] args) {
int n = 5;
int r = 2;
int p = 13;
System.out.print("Value of "+n+"C"+r+" % "+p+" is "+solve(n, r, p));
}
public static int solve(int A, int B, int C) {
if (B > A) // the value of r can never be greater than n
return 0;
if (B == 0 || B == A) // 0C0 = 1 & nCn = 1
return 1;
return (solve(A - 1, B - 1, C)%C + solve(A - 1, B, C)%C)%C;
}
}
C++
#include <bits/stdc++.h>
using namespace std;
int binomialCoeff(int n, int k, int p)
{
// Base Cases
if (k > n)
return 0;
if (k == 0 || k == n)
return 1;
// Recur
return (binomialCoeff(n - 1, k - 1, p)%p + binomialCoeff(n - 1, k, p)%p)%p;
}
int main() {
int n = 5, k = 2, p = 13;
cout << "Value of C(" << n << ", " << k << ") % " <<p<< " is " << binomialCoeff(n, k, p);
return 0;
}
Python
def binomialCoeff(n, k, p):
if k > n:
return 0
if k == 0 or k == n:
return 1
# Recursive Call
return (binomialCoeff(n-1, k-1, p)%p + binomialCoeff(n-1, k, p)%p)%p;
# Driver Program to test ht above function
n = 5
k = 2
p = 13
print ("Value of C(%d,%d) is (%d)" % (n, k,
binomialCoeff(n, k, p)))
Output
Value of 5C2 % 13 is 10
Time Complexity: O(n*max(r ,n-r))
Auxiliary Space: O(n*max(r, n-r))
But there is one problem with this code. This code is well suited to find the value of nCr only when the values of n and r are small like in our example. As soon as we try this code for a bigger value of n and r like n=50 and r=40, the result overflows and we didn’t even get a chance to take the mod of that value.
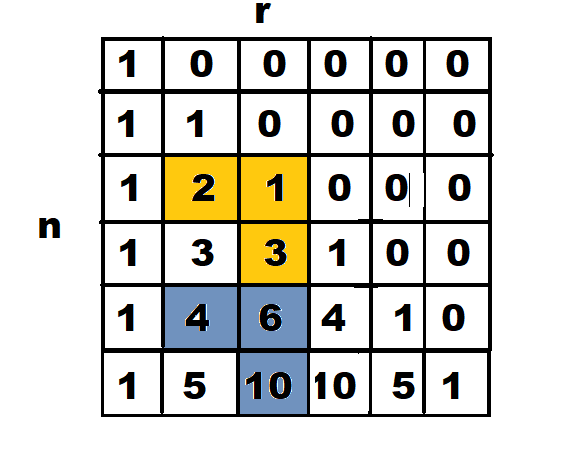
There is another problem that we can encounter with this code. This problem is not as big as the above problem but still is a problem that we should keep in mind. While doing recursion sometimes the function computes the same sub-problem again and again. See the image below

As you can see from the above image, we have 3C1 two times and 2C1 three times making it the solution to overlapping subproblems.
To deal with this overlapping and also to find an efficient solution we will use dynamic programming.
Optimized Approach using Dynamic Programming
The idea is very simple, create a 2D array using dynamic programming which stores the value of nCr using the above property of Combination – nCr = (n-1)C(r-1) + (n-1)Cr, with nC0 = nCn = 1 as base case. See the below image of the DP table
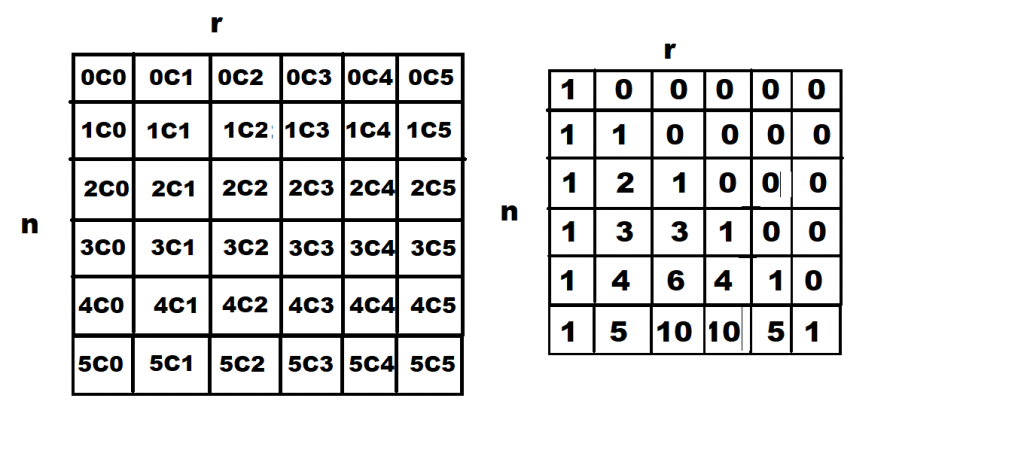
According to the formula –
nCr = (n-1)C(r-1) + (n-1)Cr
3C2 = 2C1 + 2C2
= 2 + 1 => 3 – values from the table
From the above table and the example, it is clear that we can use this dp table to make an optimized approach which can also solve our overflow problem.
Algorithm
- Make a 2D array of sizes n+1 and r+1
- Iterate for all the values of n (including n) starting from 0 and in each iteration again iterate till min(i, r) starting from 0.
- Check for the base case – nCn = nC0 = 1
- Using the Combination formula to find out the rest of the values
- Returning or print the nCr value by taking its mod.
Below is the implementation of the above-discussed approach
JAVA
package com.Tekolio.Extras;
// solve nCr%p
public class solve_cobnimatrics_1 {
public static void main(String[] args) {
int n = 5;
int r = 2;
int p = 13;
System.out.print("Value of "+n+"C"+r+" % "+p+" is "+solve(n, r, p));
}
public static int solve(int n, int k, int p) {
int D[][] = new int[n + 1][k + 1];
int i, j;
// Calculate the value of the Binomial
// Coefficient in bottom-up manner
for (i = 0; i <= n; i++) {
for (j = 0; j <= Math.min(i, k); j++) {
// Base Cases
if (j == 0 || j == i)
D[i][j] = 1;
// Calculate value using
// previously stored values
else
D[i][j] = (D[i - 1][j - 1] + D[i - 1][j])%p;
}
}
return D[n][k];
}
}
C++
#include <bits/stdc++.h>
using namespace std;
int binomialCoeff(int n, int k, int p)
{
int D[n + 1][k + 1];
int i, j;
// Calculate value of Binomial Coefficient
// in bottom up manner
for (i = 0; i <= n; i++) {
for (j = 0; j <= min(i, k); j++) {
// Base Cases
if (j == 0 || j == i)
D[i][j] = 1;
// Calculate value using previously stored values
else
D[i][j] = (D[i - 1][j - 1] + D[i - 1][j])%p;
}
}
return D[n][k];
}
// Driver Code
int main()
{
int n = 41, k = 27, p = 143;
cout << "Value of C[" << n << "][" << k << "] is "
<< binomialCoeff(n, k, p);
}
Python
def binomialCoef(n, k, p):
C = [[0 for x in range(k+1)] for x in range(n+1)]
# Calculate value of Binomial Coefficient in bottom up manner
for i in range(n+1):
for j in range(min(i, k)+1):
# Base Cases
if j == 0 or j == i:
C[i][j] = 1
# Calculate value using previously stored values
else:
C[i][j] = (C[i-1][j-1] + C[i-1][j])%p
return C[n][k]
# Driver program to test above function
n = 5
k = 2
p=13
print("Value of C[" + str(n) + "][" + str(k) + "] is "
+ str(binomialCoef(n, k, p)))
Output
Value of 5C2 % 13 is 10
Time Complexity: O(n*r)
This is because we are running a nested loop to calculate all the values of nCr which will cost us a quadratic time complexity.
Auxiliary Space: O(n*r)
Since we are making a 2D array, this is a given.
This problem is not done yet, we can optimize it further on the time complexity part but the space complexity part.
Space Optimised Solution of the above DP Approach
The idea is very simple, in the above approach we received a space complexity of O(n*r) because we have to form a 2D array to calculate each value of nCr in one go. But what if without calculating them in one go we tackle them one at a time? Though this will not reduce the time complexity as at the end of the day we still have to calculate them all but will reduce the space complexity to O(r) – linear space complexity.
Algorithm
- Make an array of r+1 size
- Initialize the base case C[0] = 1
- Iterate for all the values of n (including n) starting from 0 and in each iteration again iterate from min(i,r) to 0 to find all the values of r for that n
- Compute the value of nCr by adding the precious value with the current value
- Returning or print the nCr value by taking its mod.
JAVA
package com.Tekolio.Extras;
// solve nCr%p
public class solve_cobnimatrics_1 {
public static void main(String[] args) {
int n = 5;
int r = 2;
int p = 13;
System.out.print("Value of "+n+"C"+r+" % "+p+" is "+solve(n, r, p));
}
public static int solve(int n, int k, int p) {
int C[] = new int[k + 1];
// base case
C[0] = 1;
for (int i = 1; i <= n; i++) {
// Compute next row of pascal
// triangle using the previous row
for (int j = Math.min(i, k); j > 0; j--)
C[j] = (C[j] + C[j - 1])%p;
}
return C[k];
}
}
C++
// C++ program for space optimized Dynamic Programming
// Solution of Binomial Coefficient
#include <bits/stdc++.h>
using namespace std;
int binomialCoeff(int n, int k, int p)
{
int C[k + 1];
memset(C, 0, sizeof(C));
C[0] = 1; // nC0 is 1
for (int i = 1; i <= n; i++)
{
// Compute next row of pascal triangle using
// the previous row
for (int j = min(i, k); j > 0; j--)
C[j] = (C[j] + C[j - 1])%p;
}
return C[k]%p;
}
/* Driver code*/
int main()
{
int n = 5, r = 2, p = 13;
cout << "Value of C(" << n << "," << r << ")"<< "is " <<binomialCoeff(n, r, p);
return 0;
}
Python
def nCrModp(n, r, p):
# The array C is going to store last row of
# pascal triangle at the end. And last entry
# of last row is nCr.
C = [0 for i in range(r + 1)]
C[0] = 1 # Top row of Pascal Triangle
# One by constructs remaining rows of Pascal
# Triangle from top to bottom
for i in range(1, n + 1):
# Fill entries of current row
# using previous row values
for j in range(min(i, r), 0, -1):
# nCj = (n - 1)Cj + (n - 1)C(j - 1)
C[j] = (C[j] + C[j-1]) % p
return C[r]
# Driver Program
n = 5
r = 2
p = 13
print('Value of nCr % p is', nCrModp(n, r, p))
Output
Value of 5C2 % 13 is 10
Time Complexity: O(n*r)
This is because we are running a nested loop to calculate all the values of nCr which will cost us a quadratic time complexity.
Auxiliary Space: O(r)
We are making a 1D array to store the values of nCr
In the end, we would just say that there are many ways to solve a problem, and here I have only discussed 3 such approaches which we found simpler to understand than the others.
How do I calculate nCr%p if p is not prime?
Well, there is one way that might help you – dynamic programming. Make a dp table with all values of nCr say from 0C0 to 5C5 and then use it in conjunction with the property of combinations
nCr = n-1Cr-1 + n-1Cr

