Leaders in an array are those elements that are greater than the elements on their right-hand side in the array. This is by default true for the last element as the array end at that element and we can’t compare it with anyone.
Difficulty Level – Easy
Asked in – Microsoft and Adobe.
Let’s see an example to understand it better.
Example
Int[] arr = [16, 17, 4, 3, 5, 2]
Solution –
i=0 -> 16<17
16 is not a leader
i=1 -> 17>4, 17>3, 17>5, 17>2
17 is a leader
i=2 -> 4>3, 4<5
4 is not a leader
i=3 -> 3<5
3 is not a leader
i=4 -> 5>2
5 is a leader
i=5 -> 2 – end of the array which makes it a leader as well
Thus the leaders of the array [16, 17, 4, 3, 5, 2] are 17, 5, 2.
Observations
- The last element of the array is the leader by default
- The same goes for the largest element of the array
- Ordering doesn’t matter
How to solve it.
There are two possible methods of solving it – the brute force approach and max from the right. The brute force approach will give us a time complexity of O(n2) while the other one will give us a time complexity of O(n) – an efficient approach.
In this blog, we will use and understand both of these methods to solve this question.
Approach – I – Brute Force
As the question said, we have to find the element greater than all the elements on its right-hand side. So the brute force should be to check for all the elements if there exists an element greater than the chosen element in the array specifically on the right-hand side.
The first thing that came to mind is to use a double loop system (nested) in which the outer loop will take an element and compare it with the other elements of the array using the second or the inner loop.
Below is the Pseudo Code and the actual code for the above-discussed approach.
Pseudo Code
for i=0 to n-1
for j = i to n-1
if array[i] < array[j]
break
if j == n-1
print array[i]
JAVA
package com.Tekolio.Arrays;
public class Leaders_in_a_array {
public static void main(String[] args) {
int[] A = new int[]{16, 17, 4, 3, 5, 2};
int n = A.length;
for (int i = 0; i < n; i++) {
int j = 0;
for (j = i + 1; j < n; j++) {
if (A[j] >= A[i]) {
break;
}
}
if (j == n) {
System.out.println(A[i]);
}
}
}
}
C++
#include<iostream>
using namespace std;
/*C++ Function to print leaders in an array */
void printLeaders(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
int j;
for (j = i+1; j < size; j++)
{
if (arr[i] <=arr[j])
break;
}
if (j == size) // the loop didn't break
cout << arr[i] << " ";
}
}
/* Driver program to test above function */
int main()
{
int arr[] = {16, 17, 4, 3, 5, 2};
int n = sizeof(arr)/sizeof(arr[0]);
printLeaders(arr, n);
return 0;
}
Python
def printLeaders(arr,size):
for i in range(0, size):
for j in range(i+1, size):
if arr[i]<=arr[j]:
break
if j == size-1: # If loop didn't break
print (arr[i],end=' ')
# Driver function
arr=[16, 17, 4, 3, 5, 2]
printLeaders(arr, len(arr))
Output
17 5 2
Complexities –
Time Complexity – O(n2)
Space Complexity – O(1)
Method – II – Max from Right
We all know about the time complexities and also that O(n2) is the worst time complexity an algorithm can have. So can it be reduced to O(n)? The answer is YES, let’s see how.
So, we know that the last element of the array is always the leader. And also that any element that is greater than all other elements on its right side is the leader. So let’s scan the array from the right side keeping the track of a constant value that initially is equal to the last element of the array as it will always be the leader.
If by any chance we found an element greater than the last element, we will switch the last element with that value and again continue the same process from there. And the elements which will replace the previous value of the constant will be the leader of the array.
The time complexity for this is O(n) as we have traversed the array only once.
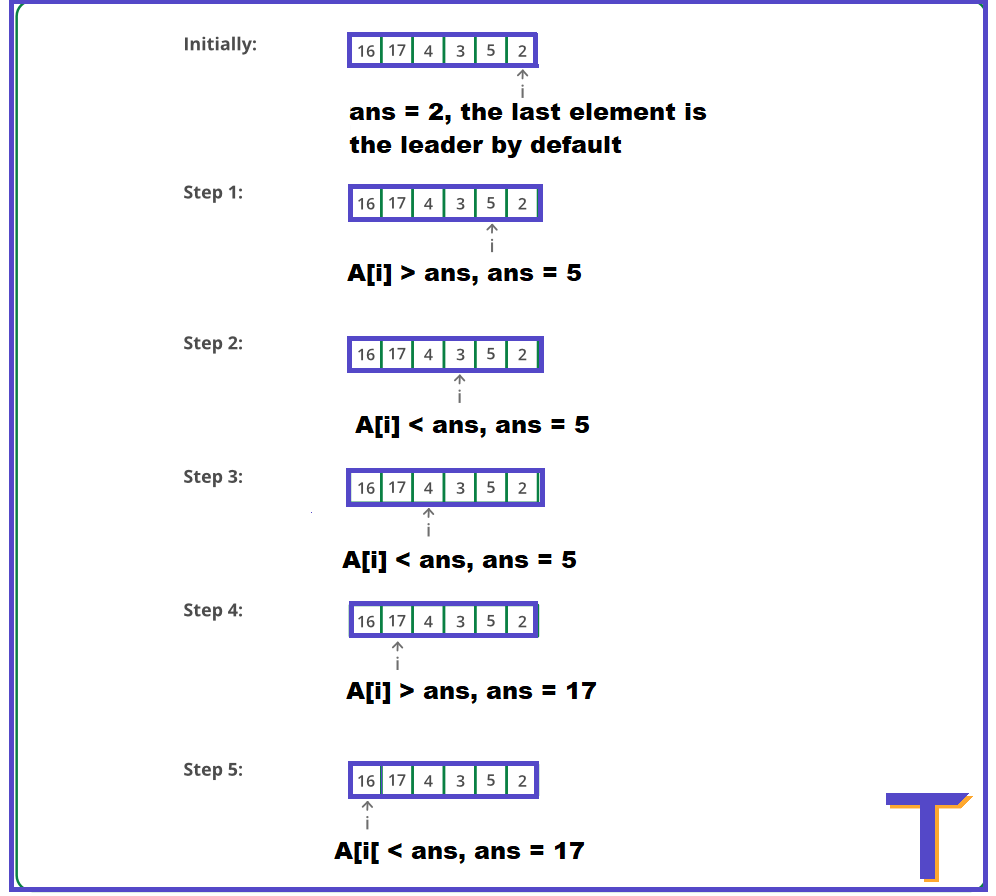
Pseudo Code
ans = leader of the array = A[n-1]
for i = n-2 to 0
if array[i] > ans
ans = array[i]
print ans
JAVA
package com.Tekolio.Arrays;
public class Leaders_in_a_array {
public static void main(String[] args) {
int[] A = new int[]{16, 17, 4, 3, 5, 2};
int n = A.length;
int ans = A[n-1];
System.out.print(ans + " ");
for(int i=n-2; i>=0; i--) {
if(ans < A[i]) {
ans = A[i];
System.out.print(ans + " ");
}
}
}
}
C++
#include <iostream>
using namespace std;
/* C++ Function to print leaders in an array */
void printLeaders(int arr[], int size)
{
int max_from_right = arr[size-1];
/* Rightmost element is always leader */
cout << max_from_right << " ";
for (int i = size-2; i >= 0; i--)
{
if (max_from_right < arr[i])
{
max_from_right = arr[i];
cout << max_from_right << " ";
}
}
}
/* Driver program to test above function*/
int main()
{
int arr[] = {16, 17, 4, 3, 5, 2};
int n = sizeof(arr)/sizeof(arr[0]);
printLeaders(arr, n);
return 0;
}
Python
def printLeaders(arr, size):
max_from_right = arr[size-1]
print (max_from_right,end=' ')
for i in range( size-2, -1, -1):
if max_from_right < arr[i]:
print (arr[i],end=' ')
max_from_right = arr[i]
# Driver function
arr = [16, 17, 4, 3, 5, 2]
printLeaders(arr, len(arr))
Output
17 5 2
Complexities –
Time Complexity – O(n)
Space Complexity – O(1)

